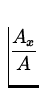Next: Displacement, Velocity and Acceleration
Up: Motion in Two Dimensions
Previous: Motion in Two Dimensions
Scalars have magnitude only. Temperature, speed, mass, and volume
are examples of scalars.
Vectors have magnitude and direction. The magnitude of
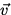 is written
|
is written
|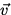 |
|  v . Position, displacement, velocity,
acceleration and force are examples of vector quantities. Vectors have the
following properties:
v . Position, displacement, velocity,
acceleration and force are examples of vector quantities. Vectors have the
following properties:
- 1.
- Vectors are equal if they have the same magnitude and
direction.
- 2.
- Vectors must have the same units in order for them to be added
or subtracted.
- 3.
- The negative of a vector has the same magnitude but
opposite direction.
- 4.
- Subtraction of a vector is defined by adding a negative
vector:
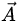 -
-  =
= 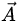 + (-
+ (-  )
)
- 5.
- Multiplication or division of a vector by a scalar
results in a vector for which
- (a)
- only the magnitude changes if the scalar is positive
- (b)
- the magnitude changes and the direction is reversed if the
scalar is negative.
- 6.
- The projections of a vector along the axes of a rectangular
co-ordinate system are called the components of the vector.
The components of a vector completely define the vector.
Figure 3.1:
Projections of a vector in 2-D.
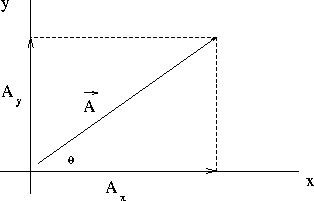 |
cos 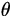
|
=
|
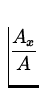 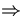 Ax = Acos Ax = Acos 
| |
sin 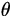
|
=
|
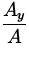 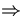 Ay = Asin Ay = Asin 
| |
We can invert these equations to find A and 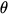 as functions of Ax
and Ay . By Pythagoras we have,
as functions of Ax
and Ay . By Pythagoras we have,
A = 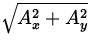
|
|
| |
and from the diagram,
- 7.
- To add vectors by components:
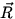 =
= 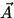 +
+ 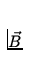 +
+ 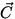 +...
+...
- (a)
- Find the components of all vectors to be added.
- (b)
- Add all x components to get
Rx = Ax + Bx + Cx + ...
Add all y components to get
Ry = Ay + By + Cy +...
- (c)
- Then




Next: Displacement, Velocity and Acceleration
Up: Motion in Two Dimensions
Previous: Motion in Two Dimensions
www-admin@theory.uwinnipeg.ca
10/9/1997
![]()
![]()
![]()
![]()
![]() is written
|
is written
|![]() |
| ![]() v . Position, displacement, velocity,
acceleration and force are examples of vector quantities. Vectors have the
following properties:
v . Position, displacement, velocity,
acceleration and force are examples of vector quantities. Vectors have the
following properties:
![]() -
- ![]() =
= ![]() + (-
+ (- ![]() )
)