Next: About this document ... Up: Motion in Two Dimensions Previous: Procedure for Solving Projectile
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Motion in Two Dimensions
Previous: Procedure for Solving Projectile

Find the sum of the following displacement vectors:
|
| = | 5.0 m at 37 o N of E | |
|
| = | 6.0 m at 45 o N of W | |
|
| = | 4.0 m at 30 o S of W | |
|
| = | 3.0 m at 60 o S of E |
Solution:
| Ax | = | 5cos 37 o = 3.99 m | |
| Ay | = | 5sin 37 o = 3.01 m | |
| Bx | = | - 6cos 45 o = - 4.24 m | |
| By | = | 6sin 45 o = 4.24 m | |
| Cx | = | - 4cos 30 o = - 3.46 m | |
| Cy | = | - 4sin 30 o = - 2.00 m | |
| Dx | = | 3cos 60 o = 1.50 m | |
| Dy | = | - 3sin 60 o = - 2.60 m |
| Rx | = | Ax + Bx + Cx + Dx = - 2.21 m | |
| Ry | = | Ay + By + Cy + Dy = 2.65 m |
|
R = | |||
|
|
![]()
The current in a river is
1.0 m/s. A woman swims 300 m
downstream and then back to her starting point without stopping. If she can
swim 2.0 m/s in still water, find the time of the round trip.
Solution:
We need to find the velocity of the woman relative to the shore for each
part of the swim. Let downstream be the positive direction and let vw be
the velocity of the water. vw/w is the velocity of the woman relative to
the water and vw/s is the velocity of the woman relative to the shore.
Then: (i) going downstream
vw/s = vw + vw/w = 1.0 + 2.0 = 3.0 m/s (ii) going
upstream
vw/s = 1.0 - 2.0 = - 1.0 m/s .
To find the time to go
300 m in each direction use
x = v0t + ![]() at 2. With a = 0 we have
t = x/v0 .
at 2. With a = 0 we have
t = x/v0 .
This gives (i) downstream:
td = 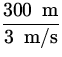 = 100 s = 100 s
|
tu = 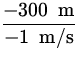 = 300 s = 300 s
|
![]()
The woman in the previous problem swims accross the river to
the opposite bank and back. The river is 300 m wide and she swims
perpendicular to the current so she ends up downstream from where she started.
Find the time for the return trip.
Solution:
Since the woman swims perpendicular to the current we can define the y-axis as
parallel to the river and treat the x and y motion independently. We are only
interested in the motion in the x-direction. For the first half of her swim
we have:
| ax | = | ||
| vx0 | = | vx = 2.0 m/s | |
| x | = | 300 m. |
t = 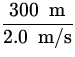 = 150 s. = 150 s.
| (3) |
![]()
(Example 3.4) A plane drops a package of emergency rations to
a stranded party of explorers. The plane is travelling horizontally at
40.0 m/s
at 100 m above the ground. Find a) where the package strikes the ground
relative to the spot it was dropped and b) the velocity of the package just
before it hits the ground.
Solution:
Set up the coordinate system as in the Figure 3.5. Consider the x and y components
separately. We are given:
| x-motion | y-motion |
| x =? | y = - 100 m |
| v0x = 40 m/s | v0y = 0 |
| ax = 0 | ay = - 9.8 m/s 2 |
| y | = |
voyt + | |
| - 100 | = |
| |
| t | = | 4.5 s. | (4) |
| x | = |
vx0t + | |
| x | = | 40(4.5) + 0 | |
| = | 180 m. | (5) |
| vy | = | vy0 + at | |
| = | 0 - 9.8(4.5) = - 44.1 m/s. |
| v | = |
| |
|
| = |
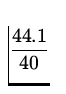 = 48 o . = 48 o .
| (6) |
![]()
A projectile is fired with an initial speed of 113 m/s at an
angle of 60 o above the horizontal from the top of a cliff 49 m
high (see Figure 3.6). Find a)
the time to reach the maximum height, b) the maximum height, c) the total time
in the air, d) the horizontal range and e) the components of the final
velocity just before the projectile hits the ground.
Solution:
Set up the coordinate system.
Consider the x- and y-motion separately. We are given:
| x-motion | y-motion |
| x =? | yB = - 49 m |
| v0x = 113cos 60 o | v0y = 113sin 60 o |
| v0x = vAx = vBx | vAy = 0 |
| ax = 0 | ay = - 9.8 m/s 2 |
| vAy | = | v0y + aytA | |
|
| = |
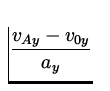
| |
| = |
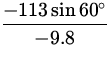 = 9.99 s. = 9.99 s.
| (7) |
| yA | = |
v0ytA + | |
| = |
113sin 60(9.99) - | (8) |
| yB | = |
v0ytB + | |
| - 49 m | = |
(113sin 60)tB - | |
|
| = | 4.9tB2 - 97.9tB - 49. | (9) |
tB = 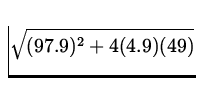 ) )
|
| xB | = |
v0xtB + | |
| = | (113cos 60)(20.5) = 1158 m. | (10) |
| vBx | = | v0x = 113cos 60 = 56.5 m/s | |
| vBy | = | v0y + aytB | |
| = | 113sin 60 - 9.8(20.5) = - 103 m/s. | (11) |
![]()
(Problem 3.50) A projectile is fired at a falling target. The
projectile leaves the gun at the same instant that the target falls from rest.
Assuming that the gun is initially aimed at the target, show that the bullet
will hit the target.
Solution:
Let xB and yB be the x and y positions of the bullet,
and
let xT and yT be the x and y positions of the target.
We
need to show that, yB = yT and xB = xT at some common time tc , the
time at which the bullet will hit the target.
The motion of the bullet is described by the two equations:
| xB | = |
v0cos | |
| yB | = |
v0sin |
|
xT = xB = v0cos |
In order for the bullet to hit the target, the y positions must be equal at
tc . The y position of the target is given by
|
yT = y0 - |
|
yB = v0sin |
To show this, consider Figure 3.7:
|
| |||
|
|
y0 = 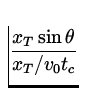 = v0sin = v0sin |
www-admin@theory.uwinnipeg.ca