Problems

$\fbox{\bf PROBLEM \thechapter.\arabic{probcount}}$

A car travelling at a constant speed of 30 m/s passes a police car at rest. The policeman starts to move at the moment the speeder passes his car and accelerates at a constant rate of 3.0 m/ s ² until he pulls even with the speeding car. Find a) the time required for the policeman to catch the speeder and b) the distance travelled during the chase.

Solution:
We are given, for the speeder:

v₀^s = 30  m/s = v ^s a ^s = 0

and for the policeman:

v₀^p =

a ^p = 3.0  m/s ².

a)

Distance travelled by the speeder x ^s = v ^st = (30)t . Distance travelled by policeman x ^p = v₀^p + ${\frac{1}{2}}$a ^pt ² = ${\frac{1}{2}}$(3.0)t ². When the policeman catches the speeder x ^s = x ^p or,

$${\textstyle\frac{1}{2}}$$

Solving for t we have t = 0 or t = ${\frac{2}{3}}$(30) = 20  s . The first solution tells us that the speeder and the policeman started at the same point at t = 0, and the second one tells us that it takes 20 s for the policeman to catch up to the speeder.

b)

Substituting back in above we find,

and,

$${\textstyle\frac{1}{2}}$$

$\fbox{\bf PROBLEM \thechapter.\arabic{probcount}}$

A car decelerates at 2.0  m/s ² and comes to a stop after travelling 25 m. Find a) the speed of the car at the start of the deceleration and b) the time required to come to a stop.

Solution:
We are given:

a = - 2.0  m/s ²

v =

x = 25  m

a)

From v ² = v₀² + 2ax we have v₀² = v ² - 2ax = - 2(- 2.0)(25) = 100  m ²/s ² or v₀ = 10  m/s.

b)

From v = v₀ + at we have t = ${\frac{1}{a}}$(v - v₀) = ${\frac{1}{-2.0}}$(- 10) = 5  s.

$\fbox{\bf PROBLEM \thechapter.\arabic{probcount}}$

A stone is thrown vertically upward from the edge of a building 19.6 m high with initial velocity 14.7 m/s. The stone just misses the building on the way down. Find a) the time of flight and b) the velocity of the stone just before it hits the ground.

Solution:
We are given,

v₀ = 14.7  m/s

a = - 9.8  m/s ²

At the time the stone hits the ground,

x = - 19.6  m

a)

From x = v₀t + ${\frac{1}{2}}$at ² we have,

$${\textstyle\frac{1}{a}} \left(-v_0\pm \sqrt{v_0^2-4(-x)\frac{1}{2}a}\right)$$ t =

$${\textstyle\frac{1}{-9.8}} \left(-14.7 \pm\sqrt{(14.7)^2 -4(19.6)\frac{1}{2}(-9.8)}\right)$$ =

$${\textstyle\frac{1}{-9.8}} \pm$$ =

The two solutions are t = 4  s and t = - 1  s. The second (negative) solution gives the time the stone would have left the ground, and is unphysical in this case. The solution we want is the first one.

b)

We substitute to find v = v₀ + at = 14.7 - 9.8(4) = - 24.5  m/s. Note that the negative velocity correctly shows that the stone is moving down.

$\fbox{\bf PROBLEM \thechapter.\arabic{probcount}}$

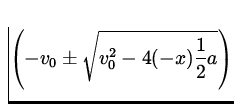
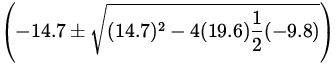
A rocket moves upward, starting from rest with an acceleration of 29.4  m/s ² for 4 s. At this time, it runs out of fuel and continues to move upward. How high does it go?

Solution:
For the first stage of the flight we are given:

v₀ =

a = 29.4  m/s ²

t = 4  s

This gives, for the velocity and position at the end of the first stage of the flight: v₁ = v₀ + at = 29.4  m/s ²(4  s ) = 117.6  m/s and x₁ = v₀t + ${\frac{1}{2}}$at ² = ${\frac{1}{2}}$(29.4)(4)² = 235.2  m.

For the second stage of the flight we start with,

v₁ = 117.6  m/s

a = - 9.8  m/s ²

and end up with v₂ = 0. We want to find the distance travelled in the second stage (x₂ - x₁). We have,

v₂² - v₁² = 2a(x₂ - x₁)

$$\Rightarrow {\textstyle\frac{1}{2a}}$$ =

$${\textstyle\frac{1}{2(-9.8)}}$$ =

= 705.6  m.

Therefore x₂ = x₁ + 705.6 = 235.2 + 705.6 = 940.8  m.