Next: About this document ... Up: Nuclear Physics Previous: Nuclear Reactions
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Nuclear Physics
Previous: Nuclear Reactions
![]()
Calculate the total binding energy of
2010 Ne.
Solution:
By Table 29.3 in the text, we see that
2010 Ne has
a mass of 19.992439 u. Since
Neon has 10 protons and 10 neutrons, the mass deficiency is
10 x 1.007825 + 10 x 1.008665 - 19.992439 = 0.172461 u .
This corresponds to an energy of
E = mc 2 = 0.172461 u x 931.5  c 2 = 160.6 MeV .
c 2 = 160.6 MeV .
![]()
Suppose you begin with
1.0 x 10- 2 g of a pure
radioactive substance and 4 h later determine that
0.25 x 10- 2 g remain. What is the half-life
of the substance?
Solution:
For this we will use the relation
N = N0e - ![]() t
t ![]()
![]() =
= ![]() t/T1/2,
t/T1/2,
 = 0.25 =
= 0.25 = ![]() t/T1/2
t/T1/2 ![]() ln 0.25 =
ln 0.25 = ![]() ln
ln  -
- ![]() ln 2,
ln 2,
![]()
The 14C content decreases after the death of a living
system with a half-life of 5739 years. If the 14C content
of an old piece of wood is found to be 12.5% of that of
an equivalent present-day sample, how old is the piece of
wood?
Solution:
This will also use the relation
N = N0e - ![]() t
t ![]()
![]() =
= ![]() t/T1/2.
t/T1/2.
0.125 = ![]() t/5739 yr
t/5739 yr ![]() ln 0.125 =
ln 0.125 =  ln
ln  -
-  ln 2,
ln 2,
![]()
Find the energy released in the alpha-decay
23892 U ![]() 23490 Th + 42 He
23490 Th + 42 He
Solution:
For this we shall need the masses
|
M | |||
|
M | |||
|
M |
238.050786 - (234.043583 + 4.002603) = 0.0046 u .
This corresponds to an energy of
E = mc 2 = 0.0046 u x 931.5  c 2 = 4.29 MeV .
c 2 = 4.29 MeV .
![]()
Suppose that the sun consists entirely of hydrogen and that
the dominant energy-releasing reaction is
4![]() 42 He + 2
42 He + 2![]() 2
2![]() +
+ ![]() .
.
Solution:
We first find the total number of hydrogen atoms in the sun by
calculating
 = 1.192 x 1057 atoms .
= 1.192 x 1057 atoms .
4 x 1.007825 - (4.002603 + 2 x 0.000549) = 0.027599 u ,
which corresponds to an energy of
E = mc 2 = 0.027599 u x 931.5  c 2 = 25.71 MeV .
c 2 = 25.71 MeV .
1.192 x 1057 atoms x 25.71  x 106
x 106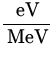 x
x  = 1.225 x 1045 J .
= 1.225 x 1045 J .
 x
x  x
x ![]() x
x  = 9.96 x 1010 yr .
= 9.96 x 1010 yr .
www-admin@theory.uwinnipeg.ca