



Next: Collisions and Kinetic Energy
Up: Momentum and Collisions
Previous: Momentum and Impulse
Momentum is conserved in any collision if the effect of any external
forces present is
negliable relative to the effect of the collision. Consider a collision as
shown in Figure (6.1).
Figure 6.1:
1-D Collision
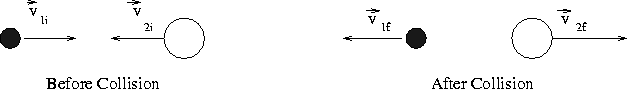 |
Apply the impulse-momentum theorem to m1 and m2 separately,
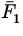  t t
|
=
|
 p1 = m1v1f - m1v1i p1 = m1v1f - m1v1i
| |
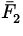  t t
|
=
|
 p2 = m2v2f - m2v2i p2 = m2v2f - m2v2i
| |
where 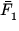 = the average force of m2 on m1 , and
= the average force of m2 on m1 , and  = the
average force of m1 on m2 . By Newton's third law
F1(t) = - F2(t)
which gives
= the
average force of m1 on m2 . By Newton's third law
F1(t) = - F2(t)
which gives
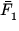 = -
= -  and so,
and so,
(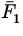 + + 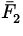 ) ) t = m1v1f - m1v1i + m2v2f - m2v2i = 0 t = m1v1f - m1v1i + m2v2f - m2v2i = 0
|
|
| |
 p1f + p2f = p1i + p2i. p1f + p2f = p1i + p2i.
|
|
| (4) |
This is the statement of the conservation of momentum.
Note:
- The system must be isolated: the affect of all external forces acting on
m1 and m2 must be negligable.
- The conservation of momentum holds for a collision involving any number
of objects:
- Momentum is a vector, and each component is conserved separately.
The equation for conservation of momentum really contains three equations,
one for each dimension.




Next: Collisions and Kinetic Energy
Up: Momentum and Collisions
Previous: Momentum and Impulse
www-admin@theory.uwinnipeg.ca
10/9/1997
![]()
![]()
![]()
![]()