Next: About this document ... Up: Introduction Previous: Coordinate Systems and Frames
![]()
![]()
![]()
![]()
Next: About this document ...
Up: Introduction
Previous: Coordinate Systems and Frames
![]()
The diameter of the earth, measured at the equator, is 7930 mi.
Express the diameter a) in meters and b) in kilometers. Use scientific
notation when expressing your answers.
Solution:
| d | = |
7930 mi ![$\displaystyle\left[ \frac{1609 \;{\:\rm m}}{1.0
\;{\:\rm mi}} \right]$](img22.gif)
| |
| = | 1.28 x 107 m |
| d | = |
1.28 x 107 m ![$\displaystyle\left[ \frac{1 \;{\:\rm km}}
{1 \times 10^{3} \;{\:\rm m}} \right]$](img23.gif)
| |
| = | 1.28 x 104 km |

The period of a simple pendulum, defined as the
time for one complete oscillation, is measured in time units and is
given by:
T = 2![]()
![]()
Solution:
![$\displaystyle\left[ 2 \pi \sqrt{\frac{l}{g}} \right]=$](img27.gif)
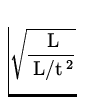 =
= ![]() = t
= t
![]()
A point is located in a polar co-ordinate system by
the co-ordinates
r = 2.5 m and
![]() = 35 o . Find the x -
and y - co-ordinates of this point, assuming that the two co-ordinate
systems have the same origin.
= 35 o . Find the x -
and y - co-ordinates of this point, assuming that the two co-ordinate
systems have the same origin.
Solution:
|
| = | cos 35 o | |
| x | = | 2.5cos 35 o = 2.05 m | |
|
[2mm] | = | sin 35 o | |
| y | = | 2.5sin 35 o = 1.43 m |
![]()
A truck driver moves up a straight mountain
highway, as shown in the figure. Elevation markers at the beginning and
ending points of the trip show that he has risen vertically 0.530 km,
and the mileage indicator on the truck shows that he has travelled
a total distance of 3.00 km during the ascent. Find the angle of
incline of the hill, ![]() .
.
Solution:
|
sin | = |
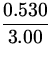 = 0.177 = 0.177
| |
|
| = |
|
www-admin@theory.uwinnipeg.ca